K 均值
Algorithm
Input
- $K$(number of clusters)
- Training set ${ x^{(1)},x^{(2)}, \dots, x^{(m)} }$
- $x^{(i)} \in \mathbb R^n$
Steps
-
Randomly initialize $K$ cluster centroids $\mu_1, \mu_2, \dots, \mu_K \in \mathbb R^n$
Optimization objective
- $c^{(i)} = \mbox{index of cluster } (1,2,\dots,K) \mbox{to witch example } x^{(i)} \mbox{ is currently assigned}$
- $\mu_k = \mbox{cluster centroid } k (\mu_k \in \mathbb R^n)$
- $\mu_{c^{(i)}} = \mbox{cluter centroid of cluter to witch example } x^{(i)} \mbox{ has been assigned}$
Objective
Random Initialization
- $\mbox{Should have } K < m$
- $\mbox{Randomly pick } K \mbox{ training examples}$
- $\mbox{Set } \mu_1,\dots,\mu_K \mbox{ equal to these } K \mbox{ examples}$
- $\mbox{Pick clustering that gave lowest cost } J(c^{(1)},\dots,c^{(m)},\mu_1,\dots,\mu_K)$
Choosing the number of clusters
Elbow method:
-
$\mbox{Choose different number of clusters like } (K=1,2,\dots,8)$
-
$\mbox{Compute the cost } J(c^{(1)},\dots,c^{(m)},\mu_1,\dots,\mu_K) \mbox{ on different K from the step 1}$
-
$\mbox{Plot (K, J) and we can find a K that the distortion goes down rapidly before it.}$
Exercise
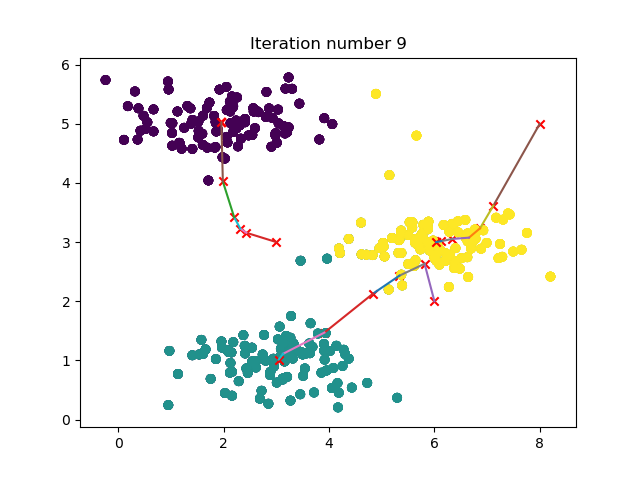
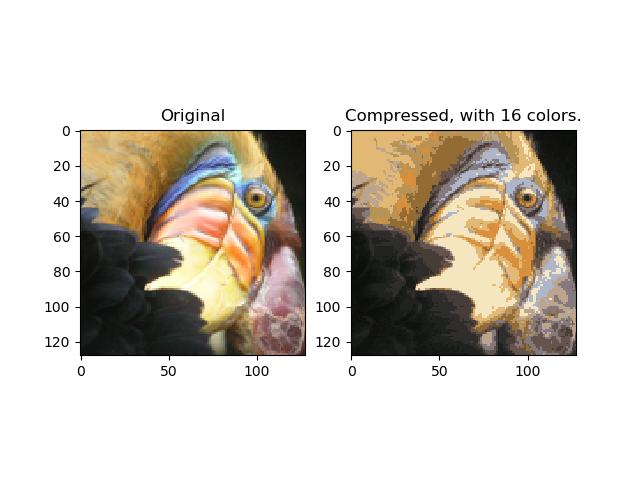
- 实验部分主要有:kmeans训练动态图示、图片压缩
k_means.py
# -*- coding: utf-8 -*-
"""
Created on Mon Jul 30 09:46:20 2018
@author: 周宝航
"""
import numpy as np
import numpy.linalg as la
import matplotlib.pyplot as plt
class KMeans(object):
def __init__(self, K, num_itres):
# cluster numbers
self.K = K
# iteration numbers
self.num_itres = num_itres
def initCentroids(self, X):
m, n = X.shape
rd = np.random.randint(0, m, self.K)
centroids = X[rd, :]
return centroids
def findClosestCentroids(self, X, centroids):
m, n = X.shape
idx = np.zeros([m, 1])
for i in range(m):
dis = [la.norm(X[i,:] - centroids[j,:]) for j in range(self.K)]
idx[i] = np.where(dis == np.min(dis))[0][0]
return np.uint8(idx)
def computeCentroids(self, X, idx):
m, n = X.shape
centroids = np.zeros([self.K, n])
for i in range(self.K):
index = (idx == i)
counts = np.sum(index)
centroids[i, :] = X.T.dot(index).T / counts
return centroids
def plotDataPoints(self, X, idx):
self.ax.scatter(X[:, 0], X[:, 1], c = idx[:, 0])
def plotProgresskMeans(self, X, centroids, previous, idx, no_i):
self.plotDataPoints(X, idx)
self.ax.scatter(centroids[:, 0].tolist(), centroids[:, 1].tolist(), c = 'r', marker = 'x')
for i in range(self.K):
data = np.r_[centroids[i, :].reshape([1,-1]), previous[i, :].reshape([1,-1])]
self.ax.plot(data[:, 0], data[:, 1])
self.ax.set_title('Iteration number {0}'.format(no_i))
def train_model(self, X, centroids, plot_progress=False):
m, n = X.shape
self.centroids = centroids
previous_centroids = self.centroids
idx = np.zeros([m, 1])
if plot_progress:
fig = plt.figure()
self.ax = fig.add_subplot(1,1,1)
for i in range(self.num_itres):
idx = self.findClosestCentroids(X, self.centroids)
if plot_progress:
self.plotProgresskMeans(X, self.centroids, previous_centroids, idx, i)
previous_centroids = self.centroids
self.centroids = self.computeCentroids(X, idx)
plt.pause(0.01)
if plot_progress:
plt.show()
return (self.centroids, idx)
main.py
# -*- coding: utf-8 -*-
"""
Created on Mon Jul 30 10:05:54 2018
@author: 周宝航
"""
from k_means import KMeans
import scipy.io as sio
import numpy as np
import matplotlib.pyplot as plt
# =================== K-Means Clustering ======================
data = sio.loadmat('data\\ex7data2.mat')
K = 3
num_iters = 10
X = data['X']
initial_centroids = np.matrix([[3,3],
[6,2],
[8,5]])
kmeans = KMeans(K, num_iters)
idx = kmeans.findClosestCentroids(X, initial_centroids)
kmeans.train_model(X, initial_centroids, True)
# ============= K-Means Clustering on Pixels ===============
data = sio.loadmat('data\\bird_small.mat')
A = data['A']
A = A / 255
m, n, _ = A.shape
X = A.reshape([-1, 3])
K = 16
num_iters = 10
kmeans = KMeans(K, num_iters)
initial_centroids = kmeans.initCentroids(X)
centroids, _ = kmeans.train_model(X, initial_centroids)
# ================= Image Compression ======================
idx = kmeans.findClosestCentroids(X, centroids)
X_recoverd = centroids[idx, :]
X_recoverd = X_recoverd.reshape([m, n, 3])
fig = plt.figure()
original = fig.add_subplot(1,2,1)
original.set_title('Original')
original.imshow(A)
compressed = fig.add_subplot(1,2,2)
compressed.set_title('Compressed, with {0} colors.'.format(K))
compressed.imshow(X_recoverd)
plt.show()
结果